Breadth First Search (BFS) Program in C

In this tutorial we will discuss about Breadth First Search or BFS program in C with algorithm and an example. Before jumping to actual coding lets discuss something about Graph and BFS.

Also Read: Depth First Search (DFS) Traversal of a Graph [Algorithm and Program]

A Graph G = (V, E) is a collection of sets V and E where V is a collection of vertices and E is a collection of edges.

A Graph can be of two types:
1. Directed Graph
2. Undirected Graph

In data structures, there is a popular term known as ‘Traversal’. It is the process of systematically visiting or examining (may be to update the Graph nodes) each node in a tree data structure, exactly once.

There are two most common methods to traverse a Graph:
1. Breadth First Search
2. Depth First Search

In this tutorial, we are going to focus on Breadth First Search technique.

In this technique, we first visit the vertex and then visit all the vertices adjacent to the starting vertex i.e., 0. Next, we pick the adjacent vertices one after another and visit their adjacent vertices and this process goes on and on until we reach the last vertex.

Breadth First Search (BFS) Example

Consider below Graph as an example.

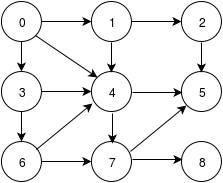
The vertex 0 is the starting vertex in our case. We start our traversal from the vertex 0. Then we will visit all vertices adjacent to vertex 0 i.e., 1, 4, 3. Here, we can visit these three vertices in any order. Suppose we visit the vertices in order 1,3,4.

The traversal would be: 0 1 3 4

Now, we shall visit all the vertices adjacent to 1, then all the vertices adjacent to 3 and then all the vertices adjacent to 4. So first we shall visit 2 (since it is adjacent to 1), then 6 (since it is adjacent to 3) and 5, 7 (since these are adjacent to 4).

Note: Vertex 4 is adjacent to vertices 1 and 3, but it has already been visited so we’ve ignored it.

The traversal would be: 0 1 3 4 2 6 5 7

Now, we shall visit all the vertices adjacent to 2, 6, 5, and 7 one by one. We can see that vertex 5 is adjacent to vertex 2. Since, it has already been traversed upon before, we have don’t need to traverse through it again and move on to the next vertex. Now, the vertices 4 and 7 are adjacent to the vertex 6. Since, they have been traversed upon before, we will not traverse on them again. Vertex 5 does not have any adjacent vertices. Vertices 5 and 8 are adjacent to vertex 7. Since, vertex 5 has been traversed upon before, we will not traverse it again. However, vertex 8 has not yet been visited. So we will traverse on vertex 8.

The traversal would be: 0 1 3 4 2 6 5 7 8

Now, we need to visit vertices adjacent to vertex 8. However, there is no vertex adjacent to vertex 8 and hence we will have to stop the traversal here.

Note: There’s no unique traversal and it can be different based on the order of the successors.

We shall look at a BFS program in C for directed Graph using a Queue. This program reaches only those vertices that are reachable from the start vertex.

Breadth First Search (BFS) Program in C

#include<stdio.h>
#include<stdlib.h>

#define MAX 100  

#define initial 1
#define waiting 2
#define visited 3

int n;    
int adj[MAX][MAX];
int state[MAX]; 
void create_graph();
void BF_Traversal();
void BFS(int v);

int queue[MAX], front = -1,rear = -1;
void insert_queue(int vertex);
int delete_queue();
int isEmpty_queue();

int main()
{
	create_graph();
	BF_Traversal();
	return 0;
}

void BF_Traversal()
{
	int v;
	
	for(v=0; v<n; v++) 
		state[v] = initial;
	
	printf("Enter Start Vertex for BFS: \n");
	scanf("%d", &v);
	BFS(v);
}

void BFS(int v)
{
	int i;
	
	insert_queue(v);
	state[v] = waiting;
	
	while(!isEmpty_queue())
	{
		v = delete_queue( );
		printf("%d ",v);
		state[v] = visited;
		
		for(i=0; i<n; i++)
		{
			if(adj[v][i] == 1 && state[i] == initial) 
			{
				insert_queue(i);
				state[i] = waiting;
			}
		}
	}
	printf("\n");
}

void insert_queue(int vertex)
{
	if(rear == MAX-1)
		printf("Queue Overflow\n");
	else
	{
		if(front == -1) 
			front = 0;
		rear = rear+1;
		queue[rear] = vertex ;
	}
}

int isEmpty_queue()
{
	if(front == -1 || front > rear)
		return 1;
	else
		return 0;
}

int delete_queue()
{
	int delete_item;
	if(front == -1 || front > rear)
	{
		printf("Queue Underflow\n");
		exit(1);
	}
	
	delete_item = queue[front];
	front = front+1;
	return delete_item;
}

void create_graph()
{
	int count,max_edge,origin,destin;

	printf("Enter number of vertices : ");
	scanf("%d",&n);
	max_edge = n*(n-1);

	for(count=1; count<=max_edge; count++)
	{
		printf("Enter edge %d( -1 -1 to quit ) : ",count);
		scanf("%d %d",&origin,&destin);

		if((origin == -1) && (destin == -1))
			break;

		if(origin>=n || destin>=n || origin<0 || destin<0)
		{
			printf("Invalid edge!\n");
			count--;
		}
		else
		{
			adj[origin][destin] = 1;
		}
	}
}

Output

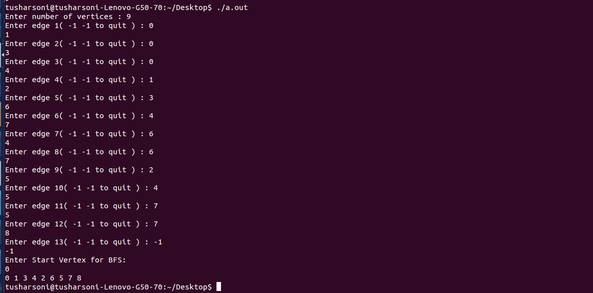
If you find anything incorrect or have any doubts regarding above Breadth First Search (BFS) program in C then comment below.