Matrix Chain Multiplication in C and C++

Here you will learn about Matrix Chain Multiplication with example and also get a program that implements matrix chain multiplication in C and C++.

Before going to main problem first remember some basis.

We know that, to multiply two matrices it is condition that, number of columns in first matrix should be equal to number of rows in second matrix. Let say there are two matrices A and B with dimensions A (2 x 3) and B (3 x 2).

Let’s see an example.

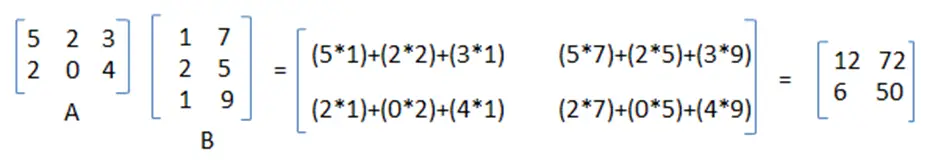
Above we can see resultant matrix is (2 x 2) matrix i.e. it contains total 4 elements. To calculate each element we did 3 multiplications (which is equal to number of columns in first matrix and number of rows in second matrix). So totally for 4 elements 4*3 = 12 multiplications are required.

In generalized way matrices A (P x Q) and B(Q x R) will result matrix (P x R) which contains P * R elements. To calculate each element need “Q” number of multiplications. Total multiplications needed are P * Q * R

Let’s try to multiply more than two matrices.

If 3 matrices A, B ,C we can find the final result in two ways (AB)C or A(BC). We get same result in any way since matrix multiplication satisfies associativity property.

Let A (1 x 2 ), B (2 x 3 ), C ( 3 x 2 ). If we follow first way, i.e. (AB)C way.

To calculate (AB) we need 1*2*3 = 6 multiplications. Now resultant AB get dimensions 1 x 3 this multiplied with C need 1*3*2 = 6 multiplications. Total 6+6 = 12 multiplications needed.

If we follow second way, i.e. A(BC) way.

To calculate (BC) we need 2*3*2 = 12 multiplications. Now resultant BC get dimensions 2 x 3. A multiplied with this result need 1*2*3 = 6. Total 12+6 = 18 multiplications needed.

Here we can observe that based on the way we parenthesize the matrices total number of multiplications are changing.

If 4 matrices A, B, C, D we can find final result in 5 ways A(B(CD)) or A((BC)(D)) or (AB)(CD) 4. ((AB)C)D or (A(BC))D. In this case also each way requires different number of multiplications.

General formula to find number of ways we can find solution is (2n)! / [ (n+1)! n! ]. After parenthesizing these many ways each way requires different number of multiplications for final result. When dimensions are large (200 x 250 like this) with more number of matrices, then finding the parenthesizing way which requires minimum number of multiplications need will gives less time complexity.

So Matrix Chain Multiplication problem aim is not to find the final result of multiplication, it is finding how to parenthesize matrices so that, requires minimum number of multiplications.

Efficient way of solving this is using dynamic programming

Matrix Chain Multiplication Using Dynamic Programming

Let we have “n” number of matrices A1, A2, A3 ……… An and dimensions are d0 x d1, d1 x d2, d2 x d3 …………. d_n-1 x d_n (i.e Dimension of Matrix A_i is d_i-1 x d_i

Solving a chain of matrix that, A_i A_i+1 A_i+2 A_i+3……. A_j= (A_i A_i+1 A_i+2 A_i+3……. A_k) (A_k+1A_k+2……. A_j) + d_i-1 d_k d_j where i <= k < j.

For more understanding check below example.

Here total i to j matrices, Matrix i to k and Matrix k+1 to j should be solved in recursive way and finally these two matrices multiplied and these dimensions d_i-1 d_k d_j(number of multiplications needed) added. The variable k is changed i to j.

Recursive Equation

Note: M[i, j] indicates that if we split from matrix i to matrix j then minimum number of scalar multiplications required.

M [ i , j ] = { 0 ; when i=j ; [means it is a single matrix . If there is only one matrix no need to multiply with any other. So 0 (zero) multiplications required.]

= { min { M[ i, k ] + M[k+1, j ] + d_i-1 d_k d_j } where i <= k< j

Example Problem

Given problem: A1 (10 x 100), A2 (100 x 20), A3(20 x 5), A4 (5 x 80)

To store results, in dynamic programming we create a table

1,1=0	2,2=0	3,3=0	4,4=0
1,2=20000	2,3=10000	3,4=8000
1,3=15000	2,4=50000
1,4=19000

This table filled using below calculations.

Here cell 2,3 stores the minimum number of scalar multiplications required to.

Using above recursive equation we can fill entire first row with all 0’s (zeros) because i=j (i.e. split happened at only one matrix which requires zero multiplications)

Table [1,2] = 10*100*20 = 20000

Table [2,3] = 100*20*5 = 10000

Table [3,4] = 20*5*80 = 8000

Table [1,3] = minimum of

= { (1,1) + (2,3) + 10* 100*5 = 0+10000+5000 = 15000

= { (1,2) + (3,3) + 10*20*5 = 20000+0+1000 = 21000

Therefore Table[1,3] is 15000 and split happened at 1

Table [2,4] = minimum of

= { (2,2) +(3,4) + 100*20*80 = 0 + 8000 + 160000 = 168000

= { (2,3) + (4,4) + 100*5*80 = 10000 + 0 + 40000 = 50000

Therefore Table of [2,4] is 50000 and split happened at 3

Table of [1,4] = minimum of

= { (1,1) +(2,4) + 10*100*80 = 0 + 50000 + 80000 = 130000

= { (1,2) +(3,4) + 10* 20* 80 = 20000 + 8000 + 16000 = 44000

= { (1,3) + (4,4) + 10*5*80 = 15000+0+4000 = 19000

Therefore table of [1,4] is 19000 which is final answer and split happened at 3.

Splitting way: (1234) is original in final outcome where 19000 answer we got split happened at 3 so ( 1 2 3 ) (4). Split for (123) means see at Table [1,3] that one minimum 15000 split at 1 . So ( ( 1 ) ( 2 3 ) ) ( 4). That means first do 2 x 3 and this 1 x first result and then this result x 4.

Time Complexity

If there are n number of matrices we are creating a table contains [(n) (n+1) ] / 2 cells that is in worst case total number of cells n*n = n² cells we need calculate = O (n²)

For each one of entry we need find minimum number of multiplications taking worst (it happens at last cell in table) that is Table [1,4] which equals to O (n) time.

Finally O (n²) * O (n) = O (n³) is time complexity.

Space Complexity

We are creating a table of n x n so space complexity is O (n²).

Program for Matrix Chain Multiplication in C

// This code implemented using Algorithm in Coremen book

#include<stdio.h>
#include<limits.h>

// Matrix Ai has dimension p[i-1] x p[i] for i = 1..n

int MatrixChainMultiplication(int p[], int n)
{
    int m[n][n];
    int i, j, k, L, q;

    for (i=1; i<n; i++)
        m[i][i] = 0;    //number of multiplications are 0(zero) when there is only one matrix

    //Here L is chain length. It varies from length 2 to length n.
    for (L=2; L<n; L++)
    {
        for (i=1; i<n-L+1; i++)
        {
            j = i+L-1;
            m[i][j] = INT_MAX;  //assigning to maximum value

            for (k=i; k<=j-1; k++)
            {
                q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
                if (q < m[i][j])
                {
                    m[i][j] = q;    //if number of multiplications found less that number will be updated.
                }
            }
        }
    }

    return m[1][n-1];   //returning the final answer which is M[1][n]

}

int main()
{
    int n,i;
    printf("Enter number of matrices\n");
    scanf("%d",&n);

    n++;

    int arr[n];

    printf("Enter dimensions \n");

    for(i=0;i<n;i++)
    {
        printf("Enter d%d :: ",i);
        scanf("%d",&arr[i]);
    }

    int size = sizeof(arr)/sizeof(arr[0]);

    printf("Minimum number of multiplications is %d ", MatrixChainMultiplication(arr, size));

    return 0;
}

// This code implemented using Algorithm in Coremen book

#include<stdio.h>

#include<limits.h>

// Matrix Ai has dimension p[i-1] x p[i] for i = 1..n

int MatrixChainMultiplication(int p[], int n)

{

int m[n][n];

int i, j, k, L, q;

for (i=1; i<n; i++)

m[i][i] = 0; //number of multiplications are 0(zero) when there is only one matrix

//Here L is chain length. It varies from length 2 to length n.

for (L=2; L<n; L++)

{

for (i=1; i<n-L+1; i++)

{

j = i+L-1;

m[i][j] = INT_MAX; //assigning to maximum value

for (k=i; k<=j-1; k++)

{

q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];

if (q < m[i][j])

{

m[i][j] = q; //if number of multiplications found less that number will be updated.

}

return m[1][n-1]; //returning the final answer which is M[1][n]

}

int main()

{

int n,i;

printf("Enter number of matrices\n");

scanf("%d",&n);

n++;

int arr[n];

printf("Enter dimensions \n");

for(i=0;i<n;i++)

{

printf("Enter d%d :: ",i);

scanf("%d",&arr[i]);

}

int size = sizeof(arr)/sizeof(arr[0]);

printf("Minimum number of multiplications is %d ", MatrixChainMultiplication(arr, size));

return 0;

}

Output

Enter number of matrices
4
Enter dimensions
Enter d0 :: 10
Enter d1 :: 100
Enter d2 :: 20
Enter d3 :: 5
Enter d4 :: 80
Minimum number of multiplications is 19000

Program for Matrix Chain Multiplication in C++

// This code implemented using Algorithm in Coremen book

#include<iostream>
#include<limits.h>

using namespace std;

// Matrix Ai has dimension p[i-1] x p[i] for i = 1..n

int MatrixChainMultiplication(int p[], int n)
{
    int m[n][n];
    int i, j, k, L, q;

    for (i=1; i<n; i++)
        m[i][i] = 0;    //number of multiplications are 0(zero) when there is only one matrix

    //Here L is chain length. It varies from length 2 to length n.
    for (L=2; L<n; L++)
    {
        for (i=1; i<n-L+1; i++)
        {
            j = i+L-1;
            m[i][j] = INT_MAX;  //assigning to maximum value

            for (k=i; k<=j-1; k++)
            {
                q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
                if (q < m[i][j])
                {
                    m[i][j] = q;    //if number of multiplications found less that number will be updated.
                }
            }
        }
    }

    return m[1][n-1];   //returning the final answer which is M[1][n]

}

int main()
{
    int n,i;
    cout<<"Enter number of matrices\n";
    cin>>n;

    n++;

    int arr[n];

    cout<<"Enter dimensions \n";

    for(i=0;i<n;i++)
    {
        cout<<"Enter d"<<i<<" :: ";
        cin>>arr[i];
    }

    int size = sizeof(arr)/sizeof(arr[0]);

    cout<<"Minimum number of multiplications is "<<MatrixChainMultiplication(arr, size));

    return 0;
}