Here you will learn about Asymptotic Analysis and Asymptotic Notations in detail.
It is common that we write Algorithm before writing code to any problem. There may exist more than one solution for a particular problem. But we need the solution which is better in time and space complexities. To compare and analyse algorithms complexities we do some analysis called Asymptotic Analysis. That is, we are concerned with the how running time of an algorithm increases with the input. Usually an algorithm asymptotically more efficient will be the best choice.
Also Read: Analysis of Algorithms
Asymptotic Notations
Asymptotic Notations are mathematical tools to represent time complexity of algorithms for asymptotic analysis.
Most commonly used three asymptotic notations are:
Big Oh Notation (O)
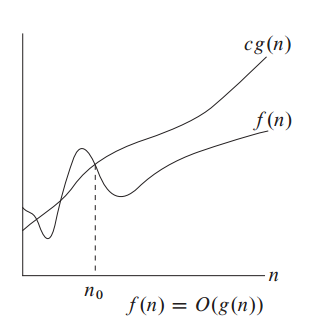
It is represented by O (capital alphabet O). See the above diagram.
The function f(n) represents that, how running time of the program is increasing when giving larger inputs to the problem.
Now, we try to find what is the worst case or upper bound of the function f(n). So we draw another function g(n) which is always greater than f(n) after some limit n = n0.
Therefore we say f(n) = O(g(n)), in the condition that, f(n) <= c g(n), where n >= n0., c > 0, n0 >= 1.
This says that f(n) is smaller than g(n).
Example
Let f(n) = 3n+2; g(n) = n. To say that f(n) = O g(n),
We need to prove that, f(n) <= cg(n); where c > 0, n0 >= 1
3n+2 <= cn; If we substitute c = 4, then 3n+2 <= 4n. If we simplify n >= 2.
Therefore for every n >= 2 and c = 4, f(n) <= c g(n). So f(n) = O g(n).
Here we proved that, n is bounding given function so definitely greater than “n”, those are n2, n3.. also upper bound this function. But as per Big-O definition, we are interested in tightest (closest) upper bound. That is the reason we write 3n+2 = O(n).
Big Omega Notation (Ω)

It is represented by Greek letter Ω.
See the above picture, the actual increasing function of the algorithm is f(n). And we want to give a lower bound for that, it is cg(n).
cg(n) is less than f(n) after some value of n = n0.
f(n) >= cg(n) , n >= n0, c > 0, n0 >= 1.
If it satisfies above conditions we say, g(n) is smaller than f(n).
Example
Let, f(n) = 3n+2. g(n) = n.
Now check can this f(n) has lower bound as g(n) or not.
f(n) = Ω g(n), this will happen only if f(n) >= c g(n).
i.e 3n+2 >= cn. Here c = 1 and n0 >= 1. This is satisfied so f(n) = Ω g(n).
Therefore, 3n+2 is lower bounded by n. Here also since n is lower bound of 3n+2, anything less than n also lower bound to 3n+2. That log(n), log log(n), like that. But as per definition we should take tightest lower bound, which is n.
Big Theta Notation (Θ)
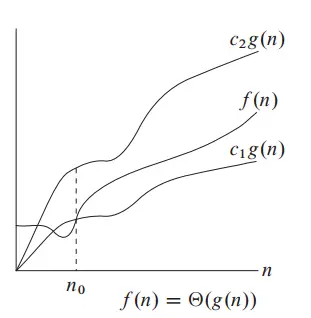
This represented by Greek letter Θ.
See the above picture, f(n) is actual growing function. We should find the both the upper bound and lower bound just by varying the constant c, with same function. Here that function is g(n).
If f(n) is bounded by c1 g(n) and c2 g(n) we can say that f(n) = Θ g(n). Constants c1 and c2 could be different.
Therefore we say f(n) = Θ g(n) , if f(n) is bounded by g(n) both in the lower and upper.
c1 g(n) <= f(n) <= c2 g(n), where c1, c2 > 0, n >= n0, n0 >= 1.
Example
F(n) = 3n+2, g(n) = n.
F(n) <= c g(n) where c = 4; That is 3n+2 <= 4n. This is valid for all n0 >= 1.
So we can say g(n) is upper bound for f(n). Now see it is as well as lower bound also.
F(n) >= c g(n); That is 3n+2 >= n. where n0 >= 1.
So both the cases are valid for this.
This theta notation also called asymptotically equal.
Applications of These Notations in Algorithms
- The Big-O notation says the worst case complexity of the algorithm. That means with any large amount of input, that program never exceeds this complexity.
- The Big-Omega notation says that best case complexity of the algorithm. That means with any small input, the program never executes less than this complexity.
- Theta notation gives the average case of complexity.
- Most of the cases we are interested in what is the worst case complexity of the program.
For more understanding, see the example below.
Let there is an array of “n” elements. We want to search an element “x” in that array.
If we do linear search we may find that element at first index i.e in Ω (1) time. This is the best case of this algorithm.
In worst case our element “x” many not exists in array. In that case we must check all elements and end up with no result. i.e O (n) time. This is the worst case of this algorithm.
Average case is, at some index of array we find that element i.e Θ (n/2) complexity.
Some common asymptotic notations are:
Constant time: O(1)
Logarithmic: O(log n)
Linear: O(n)
Quadratic: O(n2)
Cubic: O(n3)
Polynomial: nO(1)
Exponential: 2O(n)
Comment below if you have queries or found any information incorrect in above tutorial for asymptotic notations.
