In this tutorial you will learn about Hashing in C and C++ with program example. You will also learn various concepts of hashing like hash table, hash function, etc.
Hashing in Data Structure
Searching is dominant operation on any data structure. Most of the cases for inserting, deleting, updating all operations required searching first. So searching operation of particular data structure determines it’s time complexity. If we take any data structure the best time complexity for searching is O (log n) in AVL tree and sorted array only. Most of the cases it will take O (n) time. To solve this searching problem hashing concept introduced which will take O (1) time for searching. It’s constant time.
Hash Table and Hash Function
Earlier when this concept introduced programmers used to create “Direct address table”. Direct address table means, when we have “n” number of unique keys we create an array of length “n” and insert element “i” at ith index of the array. That array is called Hash Table. But due to this method even we have 10 elements of each range 1 lack, we should create table of size 1 lack for only 10 elements. Which is going to be waste of memory.
To avoid this problem we fix the size of hash table (array) and map our elements into that table using a function, called Hash function. This function decides where to put a given element into that table. If we want to search also first apply hash function decide whether the element present in hash table or not.
Example
We have numbers from 1 to 100 and hash table of size 10. Hash function is mod 10. That means number 23 will be mapped to (23 mod 10 = 3) 3rd index of hash table.
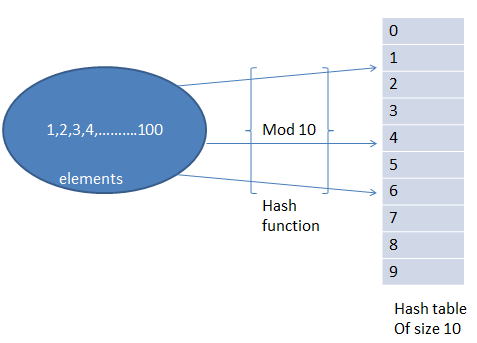
But problem is if elements (for example) 2, 12, 22, 32, elements need to be inserted then they try to insert at index 2 only. This problem is called Collision. To solve this collision problem we use different types of hash function techniques. Those are given below.
- Chaining
- Open addressing
- Linear probing
- Quadratic probing
- Double hashing
These also called collision resolution techniques.
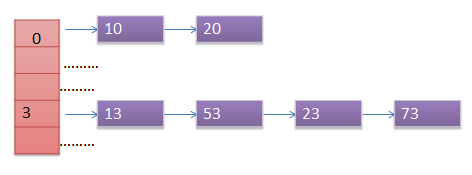
Chaining
In hash table instead of putting one element in index we maintain a linked list. When collision happened we place that element in corresponding linked list. Here some space is wasted because of pointers.
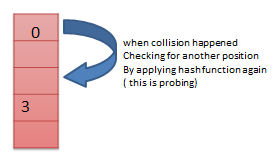
Open Addressing
In case if we have collision we again calculate the hash value using corresponding hash function. But this time we do some minor modifications to that input. This process of searching for empty space to insert element in called Probing.
Probing hash function is: h (k, i)
here k is the key value which is to be inserted. And i is number of collision with that element.
Example: If we are inserting 2, we find its hash value using h (2, 0) because it’s first collision. Suppose the answer (index) to this function index already occupied we again need to apply h (2, 1) to hash function.
Linear Probing
Let hash function is h, hash table contains 0 to n-1 slots.
Now we want to insert an element k. Apply h (k). If it results “x” and the index “x” already contain a value then we again apply hash function that h (k, 1) this equals to (h (k) + 1) mod n.
General form: h1 (k, j) = (h (k) + j) mod n
Example: Let hash table of size 5 which has function is mod 5 has already filled at positions 0, 2, 3.
Now new element 10 will try to insert. 10 mod 5 = 0. But index 0 already occupied. So it checks (probes) next (index 1) position. So 10 will insert at index 1.
Now element 11 will try to insert. 11 mod 5 = 1. But index 1 already occupied, check index 2 it also occupied (data given), 3 also occupied. So it will insert at index 4 which is empty.
We can observe that it linearly checking for next empty position. So it’s called linear probing.
Problems with linear probing:
- Primary clustering: There is a chance that continuous cells occupied, then the probability of new element insertion will get reduced. This problem is called primary clustering
- Secondary clustering: If two elements get same value at first hash function, they follow same probe sequence.
Quadratic Probing
It is same as linear probing. But when collision occurs we use different function. If collision happened that element try to occupy at quadratic distance instead of linear distance.
Due to this “Primary clustering” will be reduced. But secondary clustering won’t be eliminated.
Double Hashing
Here we use two hash functions.
h1 (k) = (h1 (k) + i h2 (k)) mod n. Here h1 and h2 are two hash functions.
Here the next prob position will depend on two functions h1 and h2 also.
Advantages by this method are there is no chance of primary clustering. And also Secondary clustering also eliminated.
Chaining vs Open Addressing
| Chaining | Open Addressing |
| Elements can be stored at outside of the table | In open addressing elements should be stored inside the table only |
| In chaining at any time the number of elements in the hash table may greater than the size of the hash table | In open addressing the number of elements present in the hash table will not exceed to number of indices in hash table. |
| In case of deletion chaining is the best method | If deletion is not required. Only inserting and searching is required open addressing is better |
| Chaining requires more space | Open addressing requires less space than chaining. |
Program for Hashing in C
Below is the implementation of hashing or hash table in C.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 |
#include<stdio.h> #include<limits.h> /* This is code for linear probing in open addressing. If you want to do quadratic probing and double hashing which are also open addressing methods in this code when I used hash function that (pos+1)%hFn in that place just replace with another function. */ void insert(int ary[],int hFn, int size){ int element,pos,n=0; printf("Enter key element to insert\n"); scanf("%d",&element); pos = element%hFn; while(ary[pos]!= INT_MIN) { // INT_MIN and INT_MAX indicates that cell is empty. So if cell is empty loop will break and goto bottom of the loop to insert element if(ary[pos]== INT_MAX) break; pos = (pos+1)%hFn; n++; if(n==size) break; // If table is full we should break, if not check this, loop will go to infinite loop. } if(n==size) printf("Hash table was full of elements\nNo Place to insert this element\n\n"); else ary[pos] = element; //Inserting element } void delete(int ary[],int hFn,int size){ /* very careful observation required while deleting. To understand code of this delete function see the note at end of the program */ int element,n=0,pos; printf("Enter element to delete\n"); scanf("%d",&element); pos = element%hFn; while(n++ != size){ if(ary[pos]==INT_MIN){ printf("Element not found in hash table\n"); break; } else if(ary[pos]==element){ ary[pos]=INT_MAX; printf("Element deleted\n\n"); break; } else{ pos = (pos+1) % hFn; } } if(--n==size) printf("Element not found in hash table\n"); } void search(int ary[],int hFn,int size){ int element,pos,n=0; printf("Enter element you want to search\n"); scanf("%d",&element); pos = element%hFn; while(n++ != size){ if(ary[pos]==element){ printf("Element found at index %d\n",pos); break; } else if(ary[pos]==INT_MAX ||ary[pos]!=INT_MIN) pos = (pos+1) %hFn; } if(--n==size) printf("Element not found in hash table\n"); } void display(int ary[],int size){ int i; printf("Index\tValue\n"); for(i=0;i<size;i++) printf("%d\t%d\n",i,ary[i]); } int main(){ int size,hFn,i,choice; printf("Enter size of hash table\n"); scanf("%d",&size); int ary[size]; printf("Enter hash function [if mod 10 enter 10]\n"); scanf("%d",&hFn); for(i=0;i<size;i++) ary[i]=INT_MIN; //Assigning INT_MIN indicates that cell is empty do{ printf("Enter your choice\n"); printf(" 1-> Insert\n 2-> Delete\n 3-> Display\n 4-> Searching\n 0-> Exit\n"); scanf("%d",&choice); switch(choice){ case 1: insert(ary,hFn,size); break; case 2: delete(ary,hFn,size); break; case 3: display(ary,size); break; case 4: search(ary,hFn,size); break; default: printf("Enter correct choice\n"); break; } }while(choice); return 0; } /* Note: Explanation for delete function and search function suppose hash table contains elements 22, 32, 42 at index positions 2, 3, 4. Now delete(22) applied. As per hash function defined we first check for index 2. Found, so deleted. And make that index to nill. Next apply delete(32). This time also it first check at index 2, but found that its nothing.Then we stop and say element 32 not found in hash table. But it's present at index 3. But how should we know whether to check to other index or not? For this when we delete any element we flag that with INT_MAX which indicates that in that position previously some element is there now it's deleted. So don't stop here your required element may present at next index. */ |
Output
Enter size of hash table
10
Enter hash function [if mod 10 enter 10]
10
Enter your choice
1-> Insert
2-> Delete
3->Display
4->Searching
0->Exit
1
Enter key element to insert
12
Enter your choice
1-> Insert
2-> Delete
3->Display
4->Searching
0->Exit
1
Enter key element to insert
22
Enter your choice
1-> Insert
2-> Delete
3->Display
4->Searching
0->Exit
1
Enter key element to insert
32
Enter your choice
1-> Insert
2-> Delete
3->Display
4->Searching
0->Exit
3
Index Value
0 -2147483648
1 -2147483648
2 12
3 22
4 32
5 -2147483648
6 -2147483648
7 -2147483648
8 -2147483648
9 -2147483648
Enter your choice
1-> Insert
2-> Delete
3->Display
4->Searching
0->Exit
2
Enter element to delete
12
Element deleted
Enter your choice
1-> Insert
2-> Delete
3->Display
4->Searching
0->Exit
4
Enter element you want to search
32
Element found at index 4
Enter your choice
1-> Insert
2-> Delete
3->Display
4->Searching
0->Exit
0
Program for Hashing in C++
Below is the implementation of hashing or hash table in C++.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 |
#include<iostream> #include<limits.h> using namespace std; /* This is code for linear probing in open addressing. If you want to do quadratic probing and double hashing which are also open addressing methods in this code when I used hash function that (pos+1)%hFn in that place just replace with another function. */ void Insert(int ary[],int hFn, int Size){ int element,pos,n=0; cout<<"Enter key element to insert\n"; cin>>element; pos = element%hFn; while(ary[pos]!= INT_MIN) { // INT_MIN and INT_MAX indicates that cell is empty. So if cell is empty loop will break and goto bottom of the loop to insert element if(ary[pos]== INT_MAX) break; pos = (pos+1)%hFn; n++; if(n==Size) break; // If table is full we should break, if not check this, loop will go to infinite loop. } if(n==Size) cout<<"Hash table was full of elements\nNo Place to insert this element\n\n"; else ary[pos] = element; //Inserting element } void Delete(int ary[],int hFn,int Size){ /* very careful observation required while deleting. To understand code of this delete function see the note at end of the program */ int element,n=0,pos; cout<<"Enter element to delete\n"; cin>>element; pos = element%hFn; while(n++ != Size){ if(ary[pos]==INT_MIN){ cout<<"Element not found in hash table\n"; break; } else if(ary[pos]==element){ ary[pos]=INT_MAX; cout<<"Element deleted\n\n"; break; } else{ pos = (pos+1) % hFn; } } if(--n==Size) cout<<"Element not found in hash table\n"; } void Search(int ary[],int hFn,int Size){ int element,pos,n=0; cout<<"Enter element you want to search\n"; cin>>element; pos = element%hFn; while(n++ != Size){ if(ary[pos]==element){ cout<<"Element found at index "<<pos<<"\n"; break; } else if(ary[pos]==INT_MAX ||ary[pos]!=INT_MIN) pos = (pos+1) %hFn; } if(--n==Size) cout<<"Element not found in hash table\n"; } void display(int ary[],int Size){ int i; cout<<"Index\tValue\n"; for(i=0;i<Size;i++) cout<<i<<"\t"<<ary[i]<<"\n"; } int main(){ int Size,hFn,i,choice; cout<<"Enter size of hash table\n"; cin>>Size; int ary[Size]; cout<<"Enter hash function [if mod 10 enter 10]\n"; cin>>hFn; for(i=0;i<Size;i++) ary[i]=INT_MIN; //Assigning INT_MIN indicates that cell is empty do{ cout<<"Enter your choice\n"; cout<<" 1-> Insert\n 2-> Delete\n 3-> Display\n 4-> Searching\n 0-> Exit\n"; cin>>choice; switch(choice){ case 1: Insert(ary,hFn,Size); break; case 2: Delete(ary,hFn,Size); break; case 3: display(ary,Size); break; case 4: Search(ary,hFn,Size); break; default: cout<<"Enter correct choice\n"; break; } }while(choice); return 0; } /* Note: Explanation for delete function and search function suppose hash table contains elements 22, 32, 42 at index positions 2, 3, 4. Now delete(22) applied. As per hash function defined we first check for index 2. Found, so deleted. And make that index to nill. Next apply delete(32). This time also it first check at index 2, but found that its nothing.Then we stop and say element 32 not found in hash table. But it's present at index 3. But how should we know whether to check to other index or not? For this when we delete any element we flag that with INT_MAX which indicates that in that position previously some element is there now it's deleted. So don't stop here your required element may present at next index. */ |
Comment below if have queries or found anything incorrect in above tutorial for Hashing in C and C++.

Useful content.I was searching for a single place where i can learn each method of hashing.Thanks:)
Are you aware that in C++ you need to have a constant for the array size declaration. When I try to run it as is I get an error because the variable “size” is not a constant value and program does not run. I am utilizing VS17’s C++ IDE
use
int *arr = new[Size];
Sorry small correction.
int *arr = new int[Size];
thank you so much it helps me a lot
all theory with basic concept gets clear with this including program
Good Explanation
While the explanation is good, the example code in C++ is simply redundant, there is no point writing a similar C++ till the time one doesn’t use object oriented approach, why you use C++ then ?
I didn’t get this part of the C implementation.Can someone enlighten me?
if(–n==size)
printf(“Element not found in hash table\n”);
how to add string values in your program?