In this tutorial you will learn about program and algorithm for infix to postfix conversion in C with an example.
In infix notation or expression operators are written in between the operands while in postfix notation every operator follows all of its operands.
Example:
Infix Expression: 5+3*2
Postfix Expression: 5 3 2*+.
Infix to Postfix Conversion Algorithm
Let Q be any infix expression and we have to convert it to postfix expression P. For this the following procedure will be followed.
1. Push left parenthesis onto STACK and add right parenthesis at the end of Q.
2. Scan Q from left to right and repeat step 3 to 6 for each element of Q until the STACK is empty.
3. If an operand is encountered add it to P.
4. If a left parenthesis is encountered push it onto the STACK.
5. If an operator is encountered, then
- Repeatedly pop from STACK and add to P each operator
which has same precedence as or higher precedence than the operator
encountered. - Push the encountered operator onto the STACK.
6. If a right parenthesis is encountered, then
- Repeatedly pop from the STACK and add to P each operator
until a left parenthesis is encountered. - Remove the left parenthesis; do not add it to P.
7. Exit
An example of converting infix expression into postfix form, showing stack status after every step is given below. Here RPN stands for reverse polish notation (postfix notation).
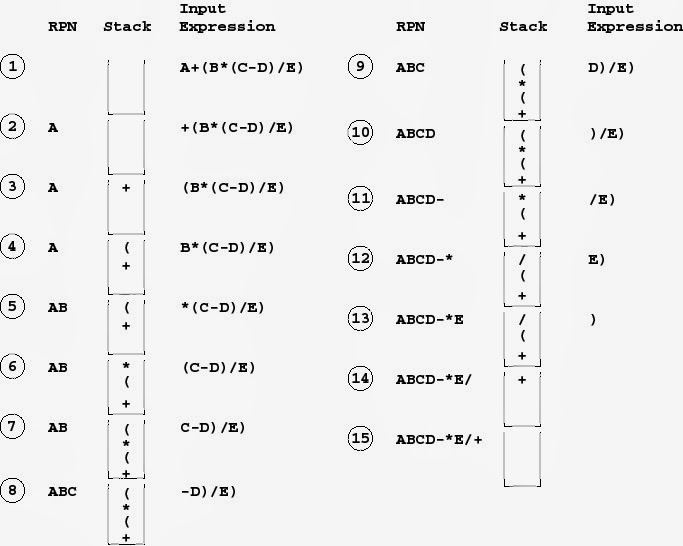
Program for Infix to Postfix Conversion in C
// Operator supported: +,-,*,/,%,^,(,)
// Operands supported: all single character operands
#include<stdio.h>
#include<conio.h>
#include<ctype.h>
#define MAX 50
typedef struct stack
{
int data[MAX];
int top;
}stack;
int precedence(char);
void init(stack *);
int empty(stack *);
int full(stack *);
int pop(stack *);
void push(stack *,int);
int top(stack *); //value of the top element
void infix_to_postfix(char infix[],char postfix[]);
void main()
{
char infix[30],postfix[30];
printf("Enter an infix expression(eg: 5+2*4): ");
gets(infix);
infix_to_postfix(infix,postfix);
printf("\nPostfix expression: %s",postfix);
}
void infix_to_postfix(char infix[],char postfix[])
{
stack s;
char x,token;
int i,j; //i-index of infix,j-index of postfix
init(&s);
j=0;
for(i=0;infix[i]!='\0';i++)
{
token=infix[i];
if(isalnum(token))
postfix[j++]=token;
else
if(token=='(')
push(&s,'(');
else
if(token==')')
while((x=pop(&s))!='(')
postfix[j++]=x;
else
{
while(precedence(token)<=precedence(top(&s))&&!empty(&s))
{
x=pop(&s);
postfix[j++]=x;
}
push(&s,token);
}
}
while(!empty(&s))
{
x=pop(&s);
postfix[j++]=x;
}
postfix[j]='\0';
}
int precedence(char x)
{
if(x=='(')
return(0);
if(x=='+'||x=='-')
return(1);
if(x=='*'||x=='/'||x=='%')
return(2);
return(3);
}
void init(stack *s)
{
s->top=-1;
}
int empty(stack *s)
{
if(s->top==-1)
return(1);
return(0);
}
int full(stack *s)
{
if(s->top==MAX-1)
return(1);
return(0);
}
void push(stack *s,int x)
{
s->top=s->top+1;
s->data[s->top]=x;
}
int pop(stack *s)
{
int x;
x=s->data[s->top];
s->top=s->top-1;
return(x);
}
int top(stack *p)
{
return (p->data[p->top]);
}
If you have any doubts regarding above infix to postfix conversion in C tutorial then feel free to comment below.
Image Credit: http://www.seas.gwu.edu/~csci133/fall04/133f04toRPN.html

It doesn’t work.
it is working
Good article.
Few observations i made:
Precedence is taken care but the asscociativity is not taken care. A+B-C will give o/p ABC-+, where as actual o/p would have been AB+C- due to left to right associativity property.
Thanks,
Shiva
thanks for the program but could u kindly explain what “return(1-3)” means or what it does and stuff
It helps in identifying the precedence of operator.
well played!!kid
It’s not working correctly for right associative operators. Check for a^b^c
Your program output is ab^c^
but output must be abc^^
its magic
Both are the same
ab^c^ = abc^^
Sir this code is very useful for me
In the picture, the stack lost “-“
I am getting an error saying “function top should have a prototype”
thanks……………………………………………..
can you upload a paragraph explaining the code because some parts of the code i coudnt understand
The example itself is giving 5+2*4 as 524 only and not 524*+ the correct answer wtf
awesome!! how to make it support multi digit and to evaluate the postfix