This tutorial is about kruskal’s algorithm in C.
It is an algorithm for finding the minimum cost spanning tree of the given graph. In kruskal’s algorithm, edges are added to the spanning tree in increasing order of cost. If the edge E forms a cycle in the spanning, it is discarded.
Also Read: Prim’s Algorithm in C [Program & Algorithm]
Kruskal’s Algorithm
This algorithm will create spanning tree with minimum weight, from a given weighted graph.
- Begin
- Create the edge list of given graph, with their weights.
- Sort the edge list according to their weights in ascending order.
- Draw all the nodes to create skeleton for spanning tree.
- Pick up the edge at the top of the edge list (i.e. edge with minimum weight).
- Remove this edge from the edge list.
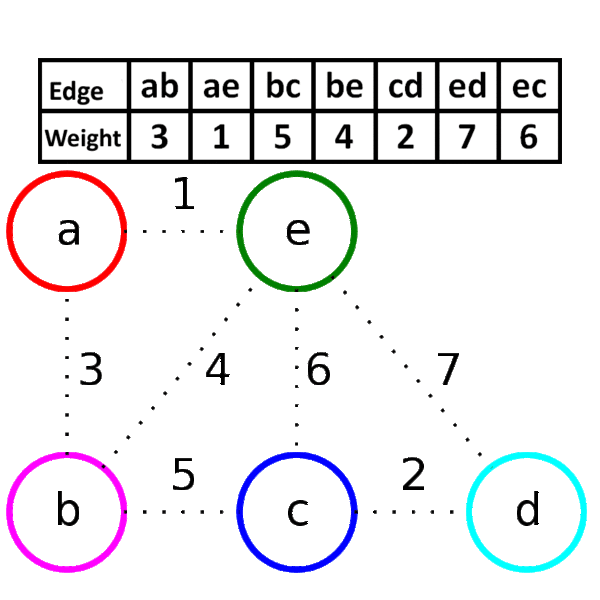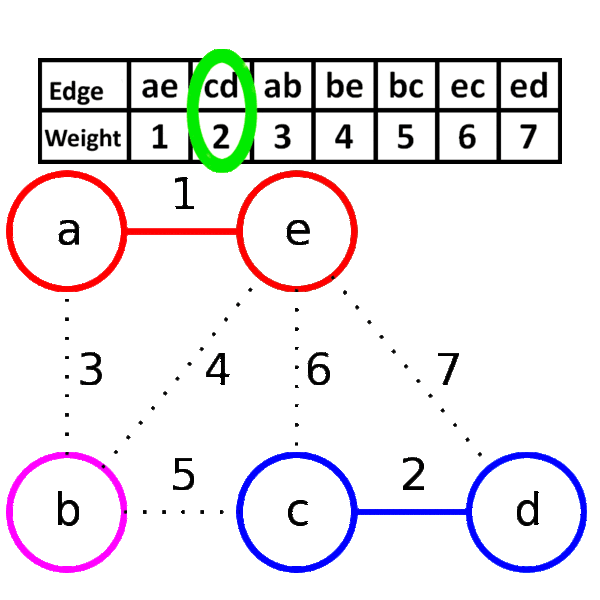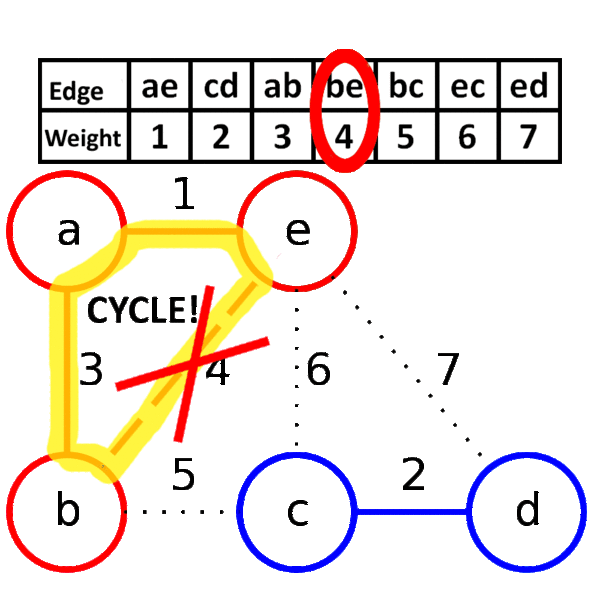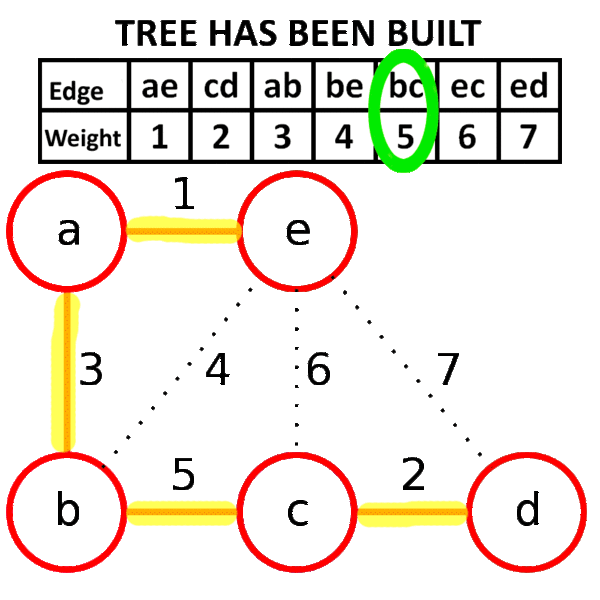
- Connect the vertices in the skeleton with given edge. If by connecting the vertices, a cycle is created in the skeleton, then discard this edge.
- Repeat steps 5 to 7, until n-1 edges are added or list of edges is over.
- Return
Program for Kruskal’s Algorithm in C
A C program for constructing a minimum cost spanning tree of a graph using Kruskal’s algorithm is given below.
#include<stdio.h>
#define MAX 30
typedef struct edge
{
int u,v,w;
}edge;
typedef struct edgelist
{
edge data[MAX];
int n;
}edgelist;
edgelist elist;
int G[MAX][MAX],n;
edgelist spanlist;
void kruskal();
int find(int belongs[],int vertexno);
void union1(int belongs[],int c1,int c2);
void sort();
void print();
void main()
{
int i,j,total_cost;
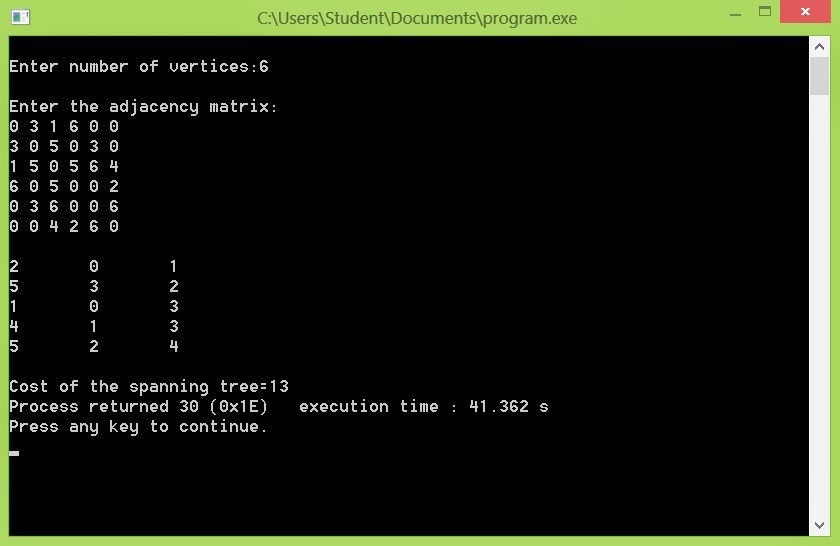
printf("\nEnter number of vertices:");
scanf("%d",&n);
printf("\nEnter the adjacency matrix:\n");
for(i=0;i<n;i++)
for(j=0;j<n;j++)
scanf("%d",&G[i][j]);
kruskal();
print();
}
void kruskal()
{
int belongs[MAX],i,j,cno1,cno2;
elist.n=0;
for(i=1;i<n;i++)
for(j=0;j<i;j++)
{
if(G[i][j]!=0)
{
elist.data[elist.n].u=i;
elist.data[elist.n].v=j;
elist.data[elist.n].w=G[i][j];
elist.n++;
}
}
sort();
for(i=0;i<n;i++)
belongs[i]=i;
spanlist.n=0;
for(i=0;i<elist.n;i++)
{
cno1=find(belongs,elist.data[i].u);
cno2=find(belongs,elist.data[i].v);
if(cno1!=cno2)
{
spanlist.data[spanlist.n]=elist.data[i];
spanlist.n=spanlist.n+1;
union1(belongs,cno1,cno2);
}
}
}
int find(int belongs[],int vertexno)
{
return(belongs[vertexno]);
}
void union1(int belongs[],int c1,int c2)
{
int i;
for(i=0;i<n;i++)
if(belongs[i]==c2)
belongs[i]=c1;
}
void sort()
{
int i,j;
edge temp;
for(i=1;i<elist.n;i++)
for(j=0;j<elist.n-1;j++)
if(elist.data[j].w>elist.data[j+1].w)
{
temp=elist.data[j];
elist.data[j]=elist.data[j+1];
elist.data[j+1]=temp;
}
}
void print()
{
int i,cost=0;
for(i=0;i<spanlist.n;i++)
{
printf("\n%d\t%d\t%d",spanlist.data[i].u,spanlist.data[i].v,spanlist.data[i].w);
cost=cost+spanlist.data[i].w;
}
printf("\n\nCost of the spanning tree=%d",cost);
}
Time Complexity of Kruskal’s Algorithm
Let us assume a graph with e number of edges and n number of vertices. Kruskal’s algorithm starts with sorting of edges.
Time complexity of sorting algorithm= O (e log e)
In Kruskal’s algorithm, we have to add an edge to the spanning tree, in each iteration. This involves merging of two components.
Time complexity of merging of components= O (e log n)
Overall time complexity of the algorithm= O (e log e) + O (e log n)
Comparison of Time Complexity of Prim’s and Kruskal’s Algorithm
The complexity of Prim’s algorithm= O(n2)
Where, n is number of vertices.
Time Complexity of Kruskal’s algorithm= O (e log e) + O (e log n)
Where, n is number of vertices and e is number of edges.
For a dense graph, O (e log n) may become worse than O (n2). Hence, the Kruskal’s algorithm should be avoided for a dense graph. Kruskal’s algorithm performs better than Prim’s algorithm for a sparse graph.
Comment below if you find anything wrong or missing in above kruskal’s algorithm in C tutorial.

Ty so much for this code….its so easy…
I love the way you handle the set tracking! The code could do with a few comments thought…
Easy version–
#include
#include
using namespace std;
int e,v;
struct Edge
{
int src,des,wt;
};
void sort1(struct Edge edge[])
{
int i, j,k;
for (i = 0; i < e-1; i++)
{
// Last i elements are already in place
for (j = 0; j edge[j+1].wt)
{
k=edge[j].wt;
edge[j].wt=edge[j+1].wt;
edge[j+1].wt=k;
k=edge[j].src;
edge[j].src=edge[j+1].src;
edge[j+1].src=k;
k=edge[j].des;
edge[j].des=edge[j+1].des;
edge[j+1].des=k;
}}
}
}
int find(int x,int parent[])
{
if(parent[x]==-1)
return x;
find(parent[x],parent);
}
void union1(int x,int y,int parent[])
{int x1,y1;
parent[x]=y;
}
int iscycle(int i ,int parent[],struct Edge edge[])
{int x,y;
x=find(edge[i].src,parent);
y=find(edge[i].des,parent);
if(x!=y)
{
union1(x,y,parent);
return 0;
}
return 1;
}
int main()
{
int i,j,k,n=0,path[745][452],sum=0;
cout<<"enter the total no of edges and vertices"<>e>>v;
int parent[v];
for(i=0;i<v;i++)
{
parent[i]=-1;
}
cout<<"enter the source, destination and weight of node "<<endl;
struct Edge edge[e];
for(i=0;i>edge[i].src>>edge[i].des>>edge[i].wt;
}
sort1(edge);
k=0;
for(i=0;i<e;i++)
{
if(!iscycle(i,parent,edge))
{
path[k][0]=edge[i].src;
path[k++][1]=edge[i].des;
n++;
sum=sum+edge[i].wt;
}
if(n==v-1)
break;
}
for(i=0;i<v-1;i++)
{
printf("%d %d",path[i][0],path[i][1]);
cout<<endl;
}
cout<<endl<<sum;
}
Great Explanation. Really easy to understand. Thanks
please can you convert this coding in java ?
Your implementations are always great and easy to understand, thank you so much!
the most complex code that i have seen in your blog made it so complex using typedef and many unnecessary snippets could have made it little simpler to understand.
There are total 5 nodes then matrix should be 5*5 not 6*6
I don’t understand the matrix the program gives as an answer. The last column is the cost but what are the first two columns?
Your code could be little modified as :
#include
#define MAX 30
typedef struct edge
{
int u,v,w;
}edge;
edge edgelist[MAX];
int G[MAX][MAX],n,e=0,s=0;
edge spanlist[MAX];
void kruskal();
int find(int belongs[],int vertexno);
void union1(int belongs[],int c1,int c2);
void sort();
void print();
int main()
{
int i,j;
printf(“\nEnter number of vertices:”);
scanf(“%d”,&n);
printf(“\nEnter the adjacency matrix:\n”);
for(i=0;i<n;i++)
for(j=0;j<n;j++)
scanf("%d",&G[i][j]);
kruskal();
print();
return 0;
}
void kruskal()
{
int belongs[MAX],i,j,cno1,cno2;
for(i=1;i<n;i++)
for(j=0;j<i;j++)
{
if(G[i][j]!=0)
{
edgelist[e].u=i;
edgelist[e].v=j;
edgelist[e].w=G[i][j];
e++;
}
}
sort();
for(i=0;i<n;i++)
belongs[i]=i;
for(i=0;i<e;i++)
{
cno1=find(belongs,edgelist[i].u);
cno2=find(belongs,edgelist[i].v);
if(cno1!=cno2)
{
spanlist[s]=edgelist[i];
s++;
union1(belongs,cno1,cno2);
}
}
}
int find(int belongs[],int vertexno)
{
return(belongs[vertexno]);
}
void union1(int belongs[],int c1,int c2)
{
int i;
for(i=0;i<n;i++)
if(belongs[i]==c2)
belongs[i]=c1;
}
void sort()
{
int i,j;
edge temp;
for(i=1;i<e;i++)
for(j=0;jedgelist[j+1].w)
{
temp=edgelist[j];
edgelist[j]=edgelist[j+1];
edgelist[j+1]=temp;
}
}
void print()
{
int i,cost=0;
for(i=0;i<s;i++)
{
printf("\n%d\t%d\t%d",spanlist[i].u,spanlist[i].v,spanlist[i].w);
cost=cost+spanlist[i].w;
}
printf("\n\nCost of the spanning tree=%d",cost);
}
Can u pls conver this code in c??
I am confused please how are you calculating the adjacent matrix.